- cross-posted to:
- askscience@lemmy.world
- cross-posted to:
- askscience@lemmy.world
cross-posted from: https://lemmy.world/post/6080744
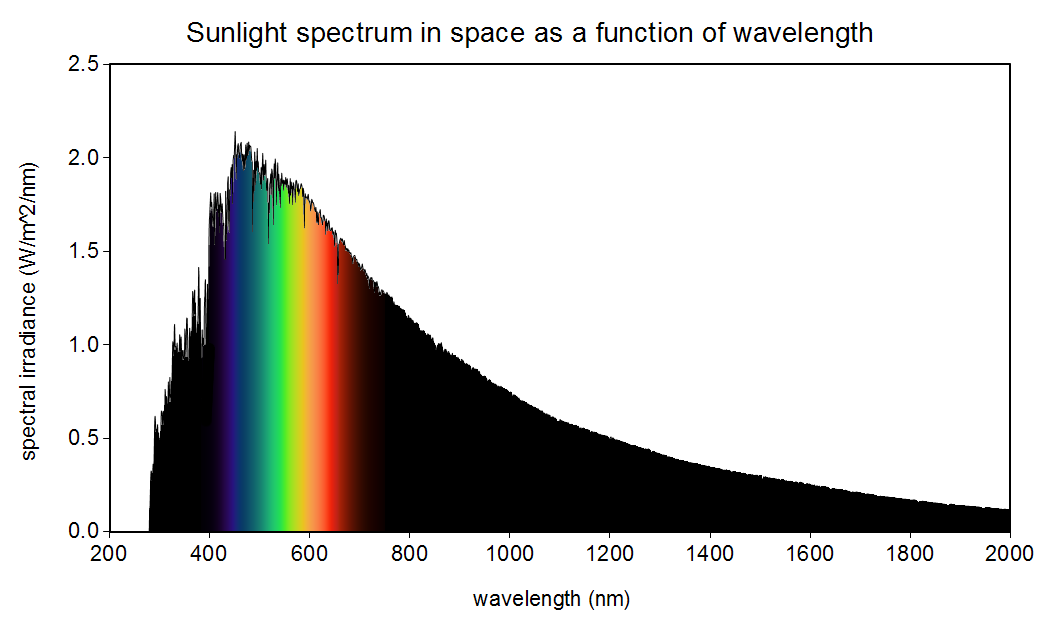
The sun is not yellow or orange as we see in books and movies. It emits all the colours in the visible spectrum (also in other spectrums as well) making it white!
It is white when seen from space. Here on Earth, the atmosphere disperses the blue part of the spectrum so that the blue sunlight comes to our eyes from all directions, making the sky blue. Without the blue light, the sun appears more yellow. So the color depends on your point of view :)
Wow, that’s really interesting! I had no idea that the atmosphere worked as a diffuser for only a small part of the spectrum like that
Yep the atmosphere is transparent to all colors of light except blue. It doesn’t absorb blue light but it does get scattered. That’s why no matter where you look in the sky, you see blue. Because the gasses there are scattering blue light in all directions, including toward you.
Isn’t that because blue is higher frequency and therefore refracts more than the other colors?
Good question. No idea. If higher frequency correlates with more scattering, then UV should also be scattered, right? Or is it something about blue visible light being just right for our mix of gases? Interesting question since that mix has changed over time. Perhaps the sky was another color during life’s early years. Is that why they’re called the Cyanobacteria? Because they turned the sky blue?
My understanding is that higher frequency == more refraction, visible or not. So in theory, x and gamma radiation should also experience more refraction. Though I wonder at what point (it any) something too high energy can somehow “pierce” through a medium rather than refracting.
It’s weird that diagrams and models of our solar system still depict the sun as yellow.
Unless you’re a kid in Japan, in which case it’s depicted as red.
It’s really a pale blue. If it were white, the visible spectrum would be pretty even, but you can see the graph is higher on the blue edge and lower on the red edge. There’s enough green and red to brighten it a lot, but it’s definitely blue.
In fact, the sun’s surface temperature is around 5800K, and you can look up what color that actually is wherever you go light bulb shopping.

This shows the colors based on temperature, and the sun is firmly in the “Day White.” It’s called white, but you can see it’s pretty clearly blue, especially next to the “Direct Sun” color.
It’s called white, but you can see it’s pretty clearly blue
It’s more complicated than that. “White” is a completely made up term, it has no physical basis. Colors are a perception, they’re not physically real. We just gave labels to some frequencies of the electromagnetic spectrum and their different combinations. And just like a camera, the human brain uses white balance correction to compensate for the fact that in different times of the day, the sunlight reaching us here on Earth has different color temperature (because it travels through different thickness of atmosphere), and by extent to compensate for different color of artificial lighting. So what our brain perceives as “white” is much dependent on context. It’s how the infamous white+gold/blue+black dress illusion works. It’s why when you put on ski goggles with orange lenses, the snow looks yellow at first but becomes “white” after a while. Then you take them off and the snow becomes momentarily blueish before it balances to white again. You can also force yourself to have the white balance temporarily out of sync in each eye.
If you printed out your chart and looked at it at different times of day or under different lighting conditions, what you’d think as neutral white would change too. So you can’t really say which white is the “true white”, it’s all relative.
Colors are a perception, true, which is why we don’t really talk about colors, we talk about wavelengths and temperature. 5800K is not white (relatively equal amounts of all visible light wavelengths), it’s light blue (decent amounts of most visible light wavelengths, but a significant peak in the 450-500nm wavelength band, which looks blue to us). Lightbulbs use color temperature because filament and halogen lights generate light the same way the sun does: by getting hot, and how hot it is determines the light wavelengths emitted. That’s why I included the chart, it’s a good analogue.
If you look at the graph provided in the OP, you can see for yourself that there’s significantly more blue than anything else being emitted.
5800K is not white…
Says who?
…(relatively equal amounts of all visible light wavelengths)
That’s the keypoint, relatively equal. You’re comparing black-body radiation temperatures but at no temperature is the spectrum actually constant across the frequencies which we call visible light. So which temperature you choose to call “white” is up to how you decide to define it. And because our eyes have different sensitivity for different frequencies, I doubt that even if you produced a perfectly constant spectral power distribution of visible light, that you would perceive it the same as what you call white on the diagram. Not to mention such a light source could be harder to find than you might think.
If you don’t believe me, you can start on Wikipedia and from there go down the rabbit hole that colors and color perception are.
(…)
A range of spectral distributions of light sources can be perceived as white—there is no single, unique specification of “white light”. For example, when buying a “white” light bulb, one might buy one labeled 2700K, 6000K, etc., which produce light having very different spectral distributions, and yet this will not prevent the user from identifying the color of objects that those light bulbs illuminate.[30]Interestingly, you can define what a perfectly white object is, with the caveat that what frequencies in what ratio actually hit your retina is again dependent on the light source.
Color vision allows us to distinguish different objects by their color. In order to do so, color constancy can keep the perceived color of an object relatively unchanged when the illumination changes among various broad (whitish) spectral distributions of light.[30]
The same principle is used in photography and cinematography where the choice of white point determines a transformation of all other color stimuli. Changes in or manipulation of the white point can be used to explain some optical illusions such as The dress.
While there is no single, unique specification of “white light”, there is indeed a unique specification of “white object”, or, more specifically, “white surface”. A perfectly white surface diffusely reflects (scatters) all visible light that strikes it, without absorbing any, irrespective of the light’s wavelength or spectral distribution.
Says who?
Says the diagram in the OP, the EM spectrum of a 5800K star, which clearly shows a peak within the visible spectrum in the blue band, and a significant (25% or so) drop off by the time it gets to the red band. Those aren’t relatively equal.
As near as I can tell, your entire argument is based on what a human being perceives to be “white”, and I’m not talking about perception at all, because it lies. Examples:
-
The sky looks blue. It’s not blue, and you can tell by looking anywhere that isn’t the sky in the daytime, because the air is the same everywhere.
-
Related: the sun looks yellow. The sun looks yellow for the same reason the sky looks blue.
-
When I close my eyes, I can’t see anything. That doesn’t mean everything is black or the same color as my eyelids.
-
Your own dress example, where different people would see different colors in the same dress.
You and I are arguing about two completely different things. You are talking about what color something looks to be, in terms of colloquial terms used to describe things people can see. I am talking about what color it is, in terms of temperature and wavelength, which are things people can measure.
Seems you didn’t get my point:
Says the diagram in the OP, the EM spectrum of a 5800K star, which clearly shows a peak within the visible spectrum in the blue band, and a significant (25% or so) drop off by the time it gets to the red band. Those aren’t relatively equal.
Then show me an EM spectrum of this mythical “white light” temperature. No matter what temperature you choose, they all have different drop-offs at different frequencies, look again at this graph I linked to before:
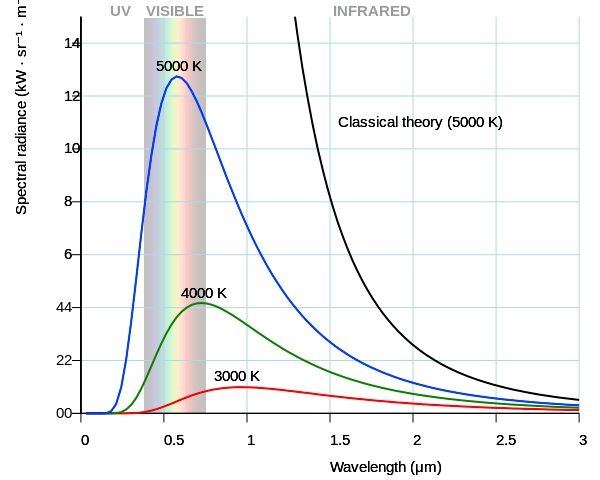
The function isn’t even symmetrical, so even if you chose one with the peak in the very middle of the visible spectrum, you’d still get different drop-offs in the blue band and in the red band. So how do you choose which temperature is this perfect white? I’ll tell you how you did, you just chose one that looked white to you. You don’t like 5800K because it looks blue to you. But it only looks blue in certain context! And there’s more, did you know that at lower luminance level, your neutral white will seem more blue?.
Additionally, you don’t need the full continuous spectrum to produce the “same” white. You can just combine single RGB wavelengths to get white for example. In fact, that’s exactly what we’re talking about as we’re presumably both looking at the image on RGB screens. But you run into the same problem, because there’s no single definition of what exact wavelength red, green or blue is, nor what their relative power should be to produce “neutral” white. But of course this “RGB white” only looks white to humans, some animals would see a different color from the full spectral white.
I am talking about what color it is
But color is perception and only that. You can talk about temperatures and wavelengths but from a physics point of view they’re just that - temperatures and wavelengths, not colors! When you go shopping for a laser, you buy a 450 nm or 473 nm or 488 nm laser. You don’t buy “blue laser” because all these three numbers are “blue”.
Color (American English) or colour (Commonwealth English) is the visual perception based on the electromagnetic spectrum. Though color is not an inherent property of matter, color perception is related to an object’s light absorption, reflection, emission spectra and interference.
(…)
Most light sources emit light at many different wavelengths; a source’s spectrum is a distribution giving its intensity at each wavelength. Although the spectrum of light arriving at the eye from a given direction determines the color sensation in that direction, there are many more possible spectral combinations than color sensations. In fact, one may formally define a color as a class of spectra that give rise to the same color sensation, although such classes would vary widely among different species, and to a lesser extent among individuals within the same species. In each such class, the members are called metamers of the color in question. This effect can be visualized by comparing the light sources’ spectral power distributions and the resulting colors.
Nerds trying to out-science each other. This is what I loved about Reddit. Thank you Lemmy, I feel at home.
-
It’s not white, it’s actually hex code FEFEFE.
I read that in the voice of Hannibal Lecter.
Am I missing something, or is the point about sunlight’s spectral peak being different in frequency space than wavelength space non-sensical?
Wavelength and frequency are simply the inverse of each other, and two different ways of describing the same color. The color with peak intensity is what it is, whether you describe it unsing wavelength or frequency.
Maybe the author meant some kind of integral / area under the curve concept, since the shape of the curve is different using wavelength vs frequency as the x axis, but even then, the actual power output across some spectrum range is independent of whether you define the range in terms of wavelength or frequency.
https://www.scielo.br/j/rbef/a/mYqvM4Qc3KLmmfFRqMbCzhB/?lang=en
This is something that bothered me when I was in undergrad but now I’ve come to understand. The article above goes through the math of computing different Wien peaks for different representations of the spectral energy density.
In short, the Wien peaks are different because what the density function measures in a given parametrization is different. In frequency space the function measures the energy radiated in a small interval [f, f + df] while in wavelength space it measure the energy radiated in an interval [λ, λ + dλ]. The function in these spaces will be different to account for the different amounts of energy radiated in these intervals, and as such the peaks are different too.
(I typed this on a phone kinda rushed so I could clarify it if you’d like)
Hey thanks for the reply! I’ll admit that paper lost me pretty quickly, so I am probably missing a subtle point. But it feels deeply unintuitive since frequency and wavelength are just two different ways of describing the same physical quantity.
So if I have a given source of photons, how the heck does the color of photons delivering most cumulative power change whether I choose to describe that color based on its wavelength or it’s frequency?
Is there an analogue to something like sound energy or is this quantum physics weirdness?
(These are semi rhetorical questions… I’m not expecting you to explain unless you really feel like it 😀)
So we can see the where this weirdness comes from when we look at the energy for a photon, E=hf=hc/λ
When we integrate we sort of slice the function in fixed intervals, what i called above df and dλ. So let’s see what is the difference in energy when our frequency interval is, for example, 1000 Hz, and use a concrete example with 100 Hz and 1100 Hz. Then ΔE = E(1100 Hz) - E(100 Hz) = h·(1100 Hz - 100 Hz) = h·(1000 Hz) = 6.626×10^-31 joules. You can check that this difference in energy will be the same if we had used any other frequencies as long as they had been 1000 Hz apart.
Now let’s do the same with a fixed interval in wavelength. We’ll use 1000 nm and start at 100 nm. Then ΔE = E(100 nm) - E(1100 nm) = hc·(1/(100 nm)-1/(1100 nm)) = 1.806×10^-18 joules. This energy corresponds to a frequency interval of 2.725×10^15 hertz. Now let’s do one more step. ΔE = E(1100 nm) - E(2100 nm) = 8.599×10^-20 joules, which corresponds to a frequency interval of 1.298×10^14 hertz.
So the energy emitted in a fixed frequency interval is not comparable to the energy emitted in a wavelength interval. To account for this the very function that is being integrated has to be different, as in the end what’s relevant is the result of the integral: the total energy radiated. This result has to be the same independent of the variable we use to integrate. That’s why the peaks in frequency are different to those in wavelength: the peaks depend on the function, and the functions aren’t the same.