If it makes you feel any better, it’s just (20 x 3) - (3 x 3).
I don’t know why, but that makes me feel better.
This must be the new math that parents are so scared of.
Back in my day, we multiplied 3 by 17 because that’s how you do it. You multiply 3 times 7, you multiply 3 times 10, and you add. Simple.
Adding three to 17, to make it 20, multiplying that by 3, and then multiplying that 3 by 3 to subtract js equally valid, and easier to work out mentally IMO. It lays the framework for good estimation skills, too.
and easier to work out mentally IMO.
And this is the key factor to why math teaching has changed. Rote memorization is actually really really awful for learning.
Teaching math used to be a case of having students fill out their times tables. I still remember having to fill out this chart in under 5 minutes:
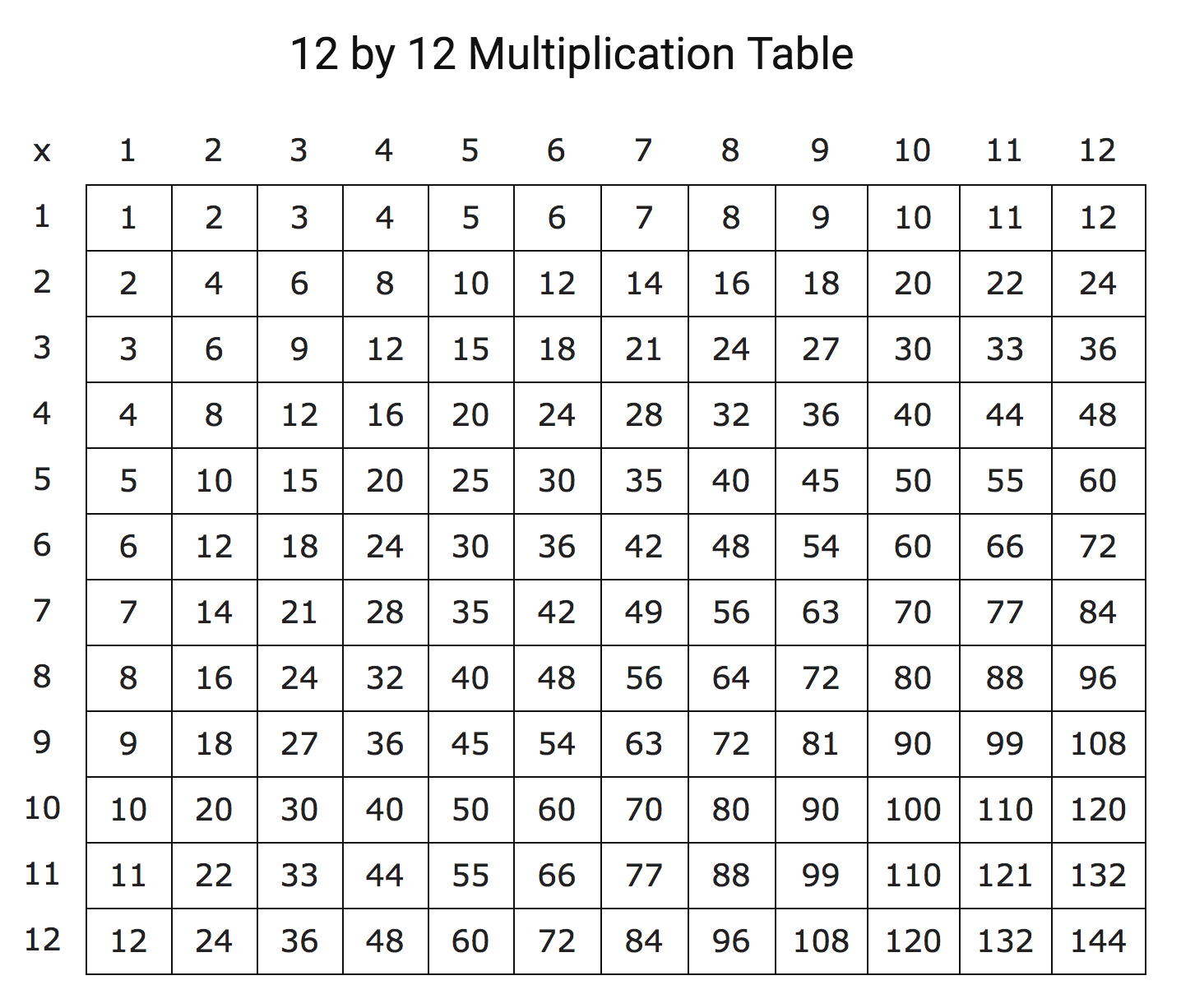
This was a quiz that we had to do multiple times per week. It was given to us blank, and 5 minutes obviously isn’t enough time to actually calculate everything; We were expected to have it memorized. And when the students had memorized the table, the quizzes changed into a series of small calculations from the table, again under 5 minutes. So if we ever had to calculate anything out, we could just refer to our memorized times table and pull the number off of that. But the issue is that this only works up to a certain point; Nobody is going to be able to reasonably memorize their times table beyond maybe 15x15. And this means that the times table essentially becomes worthless for doing math in larger numbers.
So instead, the “new” math teaches students how to take complicated problems (like 17x3) and break it down into easier steps. 17x3 is complicated, but 20x3 is just 2x3 with an added 0, and 3x3 is easy too. So if we can convert 17x3 into (20x3)-(3x3) then it becomes much easier to do in your head. Because not everyone can calculate 17x3 accurately, but virtually anyone beyond 1st grade can calculate 60-9.
The “new” math was developed by studying how the students who were good at math actually did their calculations. And it turns out, when you actually understand the concepts, you can create mental shortcuts to break the difficult problem down into a series of smaller problems. And that’s exactly what the “new” math does.
Tell me you’re not a dart player without telling me you don’t play darts.
Honestly I generally assume that everyone that isn’t a slightly portly northern English man carrying a pint does not play darts seriously
Dutch bald people
Gen X Californians for some reason
Yakuza series fan.
You could also be a genetically enhanced doctor, taught by an Irishman
I think it helps to remember that 3 times 7 is 21. When I think about that it looks less wrong.
It’s the stupid seven multiplication table. Whatever glitch in human software makes it look so much less intuitive than all the others messes with so many other things that should be easy. I swear I struggle every time I have to look at it. I had to double check seven times three multiple times right now.
I don’t think that actually helps, because it’s all vibes. 51 looks prime, because of no reason at all, and absolutely nothing looks like it should be divisible by 17, again, because raisins.
Knowing why it’s true doesn’t make it look right.
The digit sum of 51 is 6, which is divisible by three. So 51 is also divisible by three. It’s not even hard to see that it’s not prime.
Yup, my personal prime check is:
- Even?
- Ends in 5?
- Digits sum to 3?
If it fails all three and it’s not an “obvious” prime (<20), then it’s prime enough for me.
Also
Ends in 0,
but that’s covered by 5 really.
It’s also covered by being even.
But I can wrap my head around that 51 is divisible by seventeen because of 21 and seven plus something that deals with the remaining 30 somewhere.
I know that’s not how it works, but as you say it fixes my vibes when I see the 21 hiding inside the 51.
I’ll say this: the other thing that makes this one a hard pill to swallow is that 17 looks way too big, and my vibes fix doesn’t address that, but hey.
Why not add the digits? If the sum of digits is divisible by 3, the number is divisible by 3. 5 + 1 is divisible by 3, so it’s not prime.
49 “looks” more prime to me because it fails that test, and if I didn’t know it’s 72, I’d say it’s probably prime.
I think the posts along these lines are already two steps too far away from the vibes.
Nobody is even considering the number being prime, it just looks like there can’t be a round number of one against the other because one is big and ends in seven and the other is relatively small and ends in 1.
If you’re even thinking about divisibility rules you’re doing it wrong. As in, your brain is too impacted by maths to see what the numbers look like from instinct alone. There’s no thinking in this, they just look weird together.
I’ve always loved math, so seeing patterns is intuitive. 3 also happens to be my favorite number, so I like looking for it in the wild.
If someone says “51 is divisible by 17,” my instinct is that it tracks because it’s obviously divisible by 3, so the other factor would be a little less than 20. That’s literally my first instinct.
7 is a weird multiple, but 3 is really easy. I guess I’m weird…
If there’s a number that’s the most oddball in the multiplication table, it’s 7.
It’s a prime number that doesn’t share any common divisors with 10, and isn’t adjacent to a divisor of 10 either.
2 and 5 are common divisors of 10, so they’re piece of cake.
3 is so small and close to 2, so it’s not too difficult to get.
9 is one off from 10, so it has a very predictable pattern.
4, 6 and 8 are even numbers, so they share common divisors with 10.
3 is easy because of the “digits sum to 3” trick, if you get stuck counting by 3s, it’s easy to reset. Oh, and the proof for this is based on our 10-based number system, so your point absolutely stands.
There’s a drinking game called 7’s. Basically everyone has to count by 7 (first person: 7, second person: 14, third person: 21, etc) and you have to take a shot every time you get one wrong.
Right now, sober, I remember my multiplication tables really well and wouldn’t find it challenging.
But when I think of the mess that I left in the kitchen last night making a snack after drinks with friends, I can imagine the damage this game would cause.
I have to remember it in patterns.
Digits go:
7, 4, 1
8, 5, 2
9, 6, 3
0
Tens go:
0, 1, 2
2, 3, 4
4, 5, 6,
7
Then my brain recognises everything else and I can’t explain it properly 😂
100,000,001 is also divisible by 17
I’m really starting to think this 17 is not a good guy
Just wait until you find out that 17 is divisible by 17
3 is the real culprit
299,999 is divisible by 7 and 17.

:3
So simple math problems are blowing people’s minds now?
Always has been.
Just wait for the annual “PEDMAS vs PEMDAS”
discussionflame-war on any major social media platform.“Pedmas” sounds like a holiday for pedophiles…
End of debate.
Why? Not sure what the debate is, if you divide/multiply first?
It can matter if you don’t have enough significant figures, so I tend to do division last to preserve as much precision as I can. In theory it shouldn’t matter, but it can matter in practice.
So the debate is whether it could or could not matter?
No, the debate is stupid.
I’m just saying there is a situation where it could matter, not that the debate is valid.
Ah, I’m still trying to figure out what the debate is. Sorry mate, but thanks for trying to respond, I appreciate you having tried. I’m just missing something.
I am more impressed that people know about divisibility. What’s next, random people knowing about ideals?
This bugged me but then again
30 / 3 = 10 21 / 3 = 7
7+10 = 17
So yeah that makes perfect sense.
three is the first number that starts to cause problems.
Three is my favorite number, you take that back.
And 52 is divisible by 13.
Somehow less offensive.
If it bothers your OCD, think of it more as (7x3)+(10x3)=17x3=51
Or the way I do it:
- 3 * 20 = 60
- 60 - 51 = 9
- 20 - (9 / 3) = 17
So the factors are 17 and 3. I know 3 is a factor because 5+1=6, which is divisible by 3, so I just use a convenient multiple of 3 that’s pretty close to the actual number to get the divisor.
I have young kids and they keep asking me to do crazy math problems while driving, so that’s generally the trick I use.
Dude/ Dudette that’s worse. 7x3=21, 10x3=30, 21+30=
49251That does less insane to the membrane
I see them as the same except that your way illustrates what his parentheses are doing.
The way I see it the parentheses are good, it the 17x3 that hurts my brain.
It’s already broken down, then gets more complicated by the 17x3. In my mind I now need to separate 17 into 10 and 7 then multiply them each by 3 and add them together, which is where we started in the first place.
Brains are different, that’s how mine goes though.
I understood that to be a reference to the original screenshot. Thus the two equal signs. It was a way to walk you through how the breakdown ties back in.
¯\_(ツ)_/¯Not disagreeing, and I upvoted you for a different perspective. I did not see it that way, though I do now.
Like I said, brains are different.
Nah, 45 + 6
153 + 23
This is how I have always calculated in my head. It used to drive my mom and my teachers crazy when they asked me to verbalize my calculations. It was like I was hurting them somehow. I never understood why.
Dart players know this
Good news, everyone. 314159 is not evenly divisible by 17, just as you’d expect.
21 being divisible by 7 was already weird, so this just seem like more of the same.














